El objetivo de esta sección es aprender a calcular el radio de la hemiesfera que forma nuestro paracaídas.

Datos de Cálculo: Masa cansat entre 300 y 350 g, Tiempo de vuelo recomendado máximo 120 s, Velocidad de descenso entre 6 y 12 m/s (recomendadas entre 8 y 11 m/s).

Para calcular vamos a igualar la fuerza de resistencia del paracaídas (Fr) a el peso que mueve el paracaídas (Fg=mg) hacia el suelo.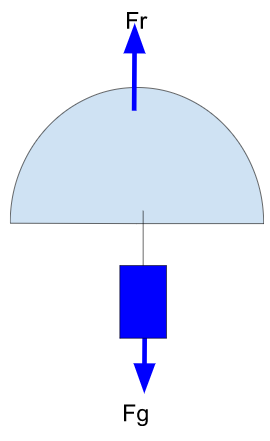 paracaídas fuerzas Cuando estén igualadas deja de acelerar y la velocidad se convierte en constante, esa es la velocidad de caída.

\( \sum F = m.a; F_{r}-F_{g}=m.a;\) como \(a=0\) para que \(V=cte \Rightarrow F_{r}=F_{g}\)

Siendo \( F_{g}=m_{cansat}.g\) (peso del cansat) y \(F_{r}=\frac{1}{2}.r.C_{d}.A.V²\) (Fuerza de resistencia del paracaídas) dónde:

r = densidad del aire (1,22 Kg/m3)
Cd = coeficiente de resistencia aerodinámico en paracaídas de forma hemiesférico, su valor es 0,62.
A = superficie del paracaídas (en nuestro caso semiesfera), \(A=2.\pi.R²\)
V = velocidad de descenso

Igualando ambas expresiones \(m_{cansat}.g=\frac{1}{2}.r.C_{d}.A.V²\), puedo despejar el área del paracaídas

\(A=\frac {2.m_{cansat}.g}{r.C_{d}.V²}\), como \(A=2.\pi.R²\), igualando \(2.\pi.R²=\frac {2.m_{cansat}.g}{r.C_{d}.V²}\), podemos despejar el Radio del paracaídas, \(R=\sqrt{\frac {2.m_{cansat}.g}{r.C_{d}.V².2.\pi}}\)

Para determinar la velocidad de caída y si la velocidad es constante (sin aceleración), tenemos que \(Velocidad=\frac{espacio}{tiempo}\), el cohete alcanza 1000 m de altura (espacio a recorrer) y el tiempo dijimos 120 s, por tanto …., ya tenemos la V. Además tenemos la masa de nuestro cansat (de 300g a 350g), con lo cual ya tenemos todo para calcular nuestro radio o diámetro de paracaídas.

Tarea: Calcula el radio de tu paracaídas

Duración:: 10
Agrupamiento:: 6

Calcula el radio o diámetro con los datos reales de tu cansat, recuerda que tienes que saber masa y velocidad de caída.

Como datos de partida voy a tener una m=350g=0,35Kg, y una velocidad de caída de \(velocidad=\frac{espacio}{tiempo}\), con un espacio (altura) de 1000 m y un vuelo de 120 segundos, nos queda \(velocidad=\frac{1000m}{120s}=8,33 \frac{m}{s}\). Sustituyendo los valores en la ecuación \(R=\sqrt{\frac {2.m_{cansat}.g}{r.C_{d}.V².2.\pi}}\), tenemos \(R=\sqrt{\frac {2.0,35Kg.9,81 \frac {m}{s²}}{1,22 \frac{Kg}{m³}.0,62.8,33² \frac{m²}{s²}.2.\pi}}=0,144m=144 mm\)